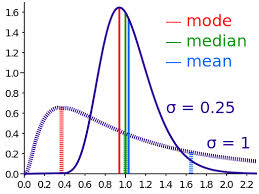
Ukuran Gejala Pusat (Definisi)

 

Ukuran gejala pusat adalah suatu ukuran yang digunakan untuk mengetahui kumpulan data mengenai sampel atau populasi yang disajikan dalam tabel atau diagram.

1. Ukuran gejala pusat adalah suatu ukuran yang digunakan untuk mengetahui kumpulan data mengenai sampel atau populasi yang disajikan dalam tabel dan diagram, yang dapat mewakili sampel atau populasi. Ada beberapa macam ukuran tendensi sentral, yaitu rata-rata (mean), median, modus, kuartil, desil dan persentil. 
2. Gejala pusat sebagai nilai rata-rata yang mempunyai kecenderungan memusat, sehingga sering disebut ukuran kecenderungan memusat (measures of central tendency). Beberapa jenis rata-rata yang sering digunakan adalah rata-rata hitung (arithmetic mean atau sering disingkat mean saja), lalu rata-rata ukur (geometric mean), kemudian rata-rata harmonis (harmonic mean). Dan umumnya terdapat istilah mean ,median, dan modus. 
3. Gejala pusat pada hakekatnya menganggap rata-rata (average) dapat merupakan nilai yang cukup representatif bagi penggambaran nilai-nilai yang terdapat dalam data yang bersangkutan. Rata-rata sedemikian itu dapat dianggap sebagai nilai sentral dan dapat digunakan sebagai pengukuran lokasi sebuah distribusi frekuensi. Statistik mengenal bermacam-macam rata-rata dengan nama-nama yang khas, yaitu rata-rata hitung (mean), median, modus, rata-rata ukur dan rata-rata harmonis itu semua merupakan jenis rata-rata yang lazim digunakan sebagai pengukuran lokasi atau pengukuran tendensi sentral (central tendency) dari sebuah distribusi.

Bersambung...
Sumber : http://vebrianaparmita.wordpress.com/2013/09/21/bab-iv-pengukuran-gejala-pusat-mean-modus-median/

Read More

TABEL KONTINGENSI

Tabel Kontingensi merupakan tabel yang digunakan untuk mengukur hubungan (asosiasi) antara dua variabel kategorik dimana tabel tersebut merangkum frekuensi bersama dari observasi pada setiap kategori variabel. Misalkan n sampel diklasifikasikan secara silang berdasarkan dua atribut dalam suatu tabel berukuran I x J, I merupakan kategori dari variabel X dan J merupakan kategori dari variabel Y. Sell pada tabel mewakili  kemungkinan IJ muncul.
Bentuk sederhana dari tabel kontongensi adalah tabel kontingesi 2 x 2 dengan format:


Sekumpulan data yang terdiri atas dua faktor atau dua variabel, faktor yang satu terdiri atas b kategori dan lainnya terdiri atas k kategori, maka dapat dibuat suatu tabel kontingensi berukuran b x k dengan b menyatakan baris dan k menyatakan kolom. Bentuk yang sering dipakai dapat dilihat berikut ini.

BANYAK MURID SEKOLAH DI DAERAH AMBULU

MENURUT TINGKAT SEKOLAH DAN JENIS KELAMIN

TAHUN 2006

              Tingkat Sekolah

JENIS KELAMIN	SD	SMP	SMA	JUMLAH
Laki – laki	4756	2795	1459	9012
Perempuan	4032	2116	1256	7404
Jumlah	8790	4911	2715	16416

Catatan : Data karangan

Daftar kontingensi diatas adalah merupakan tabel kontingensi 2 x 3 karena terdiri atas 2 baris dan 3 kolom.

Model lain, misalnya tabel kontingensi 4 x 4, dapat dilihat pada tabel berikut.

HASIL UJIAN MATEMATIKA DAN FISIKA

UNTUK 100 SISWA SMA

NILAI MATEMATIKA NILAI STATISTIKA	50 - 59	60 - 69	70 - 79	80 - 89	JUMLAH
60 – 69	12	7	10	2	31
70 – 79	8	10	5	7	30
80 – 89	10	8	3	3	24
90 – 99	5	3	12	2	22
JUMLAH	35	28	30	14	107

Ctatatan : Data karangan


Hipotesis yang diajukan adalah
H₀ : Tidak ada hubungan antara variabel 1 dan variabel 2 atau variabel 1 dan variabel 2 saling bebas (independen)
H₁: Tidak ada hubungan antara variabel 1 dan variabel 2 atau variabel 1 dan variabel 2 saling bebas (independen)

Tolak hipotesis nol(H₀) jika nilai statistik uji diatas lebih besar dari nilai kritis distribusi chi-square dengan derajat bebas (2-1)(2-1)=1 pada tingkat signifikansi alpha (α) tertentu yang berarti terdapat hubungan antara variabel 1 dengan variabel 2.

Hipotesis nol(H₀) ditolak jika nilai statistik uji diatas lebih besar dari nilai kritis distribusi chi-square dengan derajat bebas (I-1)(J-1) pada tingkat signifikansi alpha (α) tertentu yang berarti terdapat hubungan antara variabel 1 dengan variabel 2.
Contoh: Pada liga bola basket professional selama 1980  –  1982, yaitu ketika Larry Bird dari Boston Celtics melakukan lemparan bebas (pada basket lemparan bebas adalah 2 kali lemparan). Catatan lemparan bebas Larry Birds adalah 5 kali dia gagal memasukkan keduanya, 251 kali dia berhasil memasukkan keduanya, 34 kali dia berhasil hanya pada lemparan pertama, dan 48 kali dia berhasil hanya pada lemparan kedua. Apakah masuk akal bahwa lemparan bebas tersebut adalah independen ?
Jawab:
Hal pertama yang harus dilakukan adalah mengidentifikasi bagaimana bentuk tabel yang akan dibuat. Tabel Kontingensi untuk kasus di atas sebagai berikut

Karena yang ingin dilihat apakah masuk akal mengatakan bahwa lemparan bebas yang dilakukan tersebut saling independen maka pengujian yang dilakukan adalah sebagai berikut:

Uji Statistik (perhitungan) :
Terlebih dahulu hitung frekuensi harapan untuk masing-masing sel pada tabel kontingensi.



Uji dengan  menggunakan Chi-Square seperti yang diatas hanya bisa digunakan jika tidak lebih 20 % frekuensi harapan dari sel yang ada pada tabel kurang dari 5  dan tidak boleh ada satupun dari sel memiliki frekuensi harapan kurang dari 1. Apabila persyaratan diatas tidak bisa terpenuhi, maka kita dapat memperbesar nilai frekuensi harapannya dengan jalan menggabungkan baris atau kolom yang saling berdampingan. Penggabungan yang dilakukan harus secara wajar dan memiliki makna. Namun hal ini tidak dapat diterapkan untuk table kontingensi 2×2, sebagai alternatifnya kita bisa  menggunkan Uji Fisher yang memang dikhususkan untuk jumlah sampel yang kecil.
Peniliti biasanya dapat menghindari masalah ini dengan merancang sebelumnya untuk mengumpulkan sejumlah kasus yang cukup besar sehubungan dengan banyak klasifikasi yang ingin digunakan dalam penelitiannya.

Sumber : http://parameterd.wordpress.com/2013/09/13/tabel-kontingensi-cross-classification-table/

Read More

DIAGRAM LINGKARAN

Untuk membuat diagram lingkaran, gambarkan sebuah lingkaran, lalu bagi – bagi menjadi beberapa sector. Tiap sector melukiskan kategori data yang terlebih dahulu diubah kedalam derajat. Dianjurkan titik pembagian mulai dari titik tertinggi lingkaran. Diagram lingkaran ini sering digunakan untuk melukiskan data atribut.

Contoh :

BIAYA TIAP BULAN SMP AMBULU

KEPERLUAN BIAYA
POS	PERSENTASE (%)
A B C D E F	28 18 14 22 10 8

                   Catatan : Data karangan

Terlebih dahulu tiap nilai data diubah kedalam derajat, sehingga diperoleh tabel berikut.

BIAYA TIAP BULAN SMP AMBULU

KEPERLUAN BIAYA
POS	PERSENTASE (%)	DERAJAT
A	28	(28/100) X 360 O = 100,8 O
B	18	(18/100) X 360 O = 64,8 O
C	14	(14/100) X 360 O = 50,4 O
D	22	(22/100) X 360 O = 79,2 O
E	10	(10/100) X 360 O = 36 O
F	8	(8/100) X 360 O = 28,8 O

Read More

DIAGRAM GARIS

Diagram garis merupakan diagram yang digunakan untuk menggambarkan keadaan yang serba terus atau berkesinambungan, misalnya produksi minyak tiap tahun, jumlah penduduk tiap tahun, dsb. Diagram garis juga memiliki sumbu datar dan sumbu tegak, dimana sumbu datar menyatakan waktu dan sumbu tegak menyatakan kuantum data.

Contoh dibawah ini menyatakan penggunaan barang di sebuah perusahaan selama tahun 1971 – 1980 yang diagramnya tertera dalam gambar 2.6.

  

PENGGUNAAN BARANG HABIS PAKAI DI PERUSAHAAN A

(DALAM SATUAN)

TAHUN 1971 – 1980

TAHUN	BARANG YANG DIGUNAKAN
1971 1972 1973 1974 1975 1976 1977 1978 1979 1980	376 524 412 310 268 476 316 556 585 434

     Catatan : Data karangan

Read More

DIAGRAM BATANG

Penyajian dalam bentuk gambar grafik atau diagram dapat lebih menjelaskan lagi persoalan secara visual. Diagram batang (histogram) adalah gambaran mengenai suatu distribusi frekuensi, dimana untuk setiap kelas dinyatakan dalam skala horizontal (datar) dan frekuensinya dalam skala vertical (tegak); atau sebaliknya. Data yang variabelnya berbentuk kategori atau atribut sangat tepat disajikan dengan diagram batang. Jika diagram dibuat tegak, maka sumbu datar dipakai untuk menyatakan atribut. Kuantum atau nilai data digambar pada sumbu tegak. Perhatikan contoh berikut.

JUMLAH SISWA MENURUT TINGKAT SEKOLAH DAN JENIS KELAMIN

TINGKAT SEKOLAH	JUMLAH SISWA		JUMLAH
	LAKI – LAKI	PEREMPUAN
SD SMP ST SMA SMK	875 512 347 476 316	687 507 85 342 427	1.562 1.019 432 818 743
TOTAL	2.526	2.048	4.574

     Catatan : Data karangan

Kalau hanya diperhatikan jumlah siswa tanpa perincian jenis kelamin, diagramnya merupakan diagram batang tunggal, seperti Gambar 1.

Letak batang yang satu dengan yang lainnya harus terpisah dan lebarnya digambarkan serasi dengan tempat diagram. Diatas batang boleh juga nilai kuantum data dituliskan.

Gambar 1

Mungkin juga diagram batang dibuat secara horizontal, lihat gambar 2.

Gambar 2

Jika jenis kelamin juga diperhatikan dan digambarkan diagramnya, maka didapat diagram batang dua komponen. Bentuk diagram vertical dan horisontalnya dapat dilihat pada gambar 3 dan gambar 4 berikut.

Gambar 3

Gambar 4

 Gambar 5

Read More