Tabel Kontingensi merupakan tabel yang digunakan untuk mengukur hubungan (asosiasi) antara dua variabel kategorik dimana
tabel tersebut merangkum frekuensi bersama dari observasi pada setiap
kategori variabel. Misalkan n sampel diklasifikasikan secara silang
berdasarkan dua atribut dalam suatu tabel berukuran I x J, I merupakan
kategori dari variabel X dan J merupakan kategori dari variabel Y. Sell
pada tabel mewakili kemungkinan IJ muncul.
Bentuk sederhana dari tabel kontongensi adalah tabel kontingesi 2 x 2 dengan format:
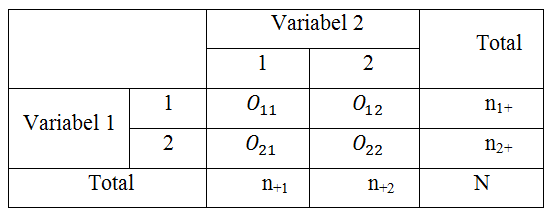
Sekumpulan data yang terdiri atas dua faktor atau dua variabel, faktor yang satu terdiri atas b kategori dan lainnya terdiri atas k kategori, maka dapat dibuat suatu tabel kontingensi berukuran b x k dengan b menyatakan baris dan k menyatakan kolom. Bentuk yang sering dipakai dapat dilihat berikut ini.
Bentuk sederhana dari tabel kontongensi adalah tabel kontingesi 2 x 2 dengan format:

Sekumpulan data yang terdiri atas dua faktor atau dua variabel, faktor yang satu terdiri atas b kategori dan lainnya terdiri atas k kategori, maka dapat dibuat suatu tabel kontingensi berukuran b x k dengan b menyatakan baris dan k menyatakan kolom. Bentuk yang sering dipakai dapat dilihat berikut ini.
BANYAK MURID SEKOLAH DI DAERAH AMBULU
MENURUT TINGKAT SEKOLAH DAN JENIS KELAMIN
TAHUN 2006
Tingkat Sekolah
JENIS KELAMIN
|
SD
|
SMP
|
SMA
|
JUMLAH
|
Laki – laki
|
4756
|
2795
|
1459
|
9012
|
Perempuan
|
4032
|
2116
|
1256
|
7404
|
Jumlah
|
8790
|
4911
|
2715
|
16416
|
Catatan : Data karangan
Daftar kontingensi diatas adalah merupakan tabel kontingensi 2 x 3 karena terdiri atas 2 baris dan 3 kolom.
Model lain, misalnya tabel kontingensi 4 x 4, dapat dilihat pada tabel berikut.
HASIL UJIAN MATEMATIKA DAN FISIKA
UNTUK 100 SISWA SMA
NILAI
MATEMATIKA
NILAI
STATISTIKA
|
50 - 59
|
60 - 69
|
70 - 79
|
80 - 89
|
JUMLAH
|
60 – 69
|
12
|
7
|
10
|
2
|
31
|
70 – 79
|
8
|
10
|
5
|
7
|
30
|
80 – 89
|
10
|
8
|
3
|
3
|
24
|
90 – 99
|
5
|
3
|
12
|
2
|
22
|
JUMLAH
|
35
|
28
|
30
|
14
|
107
|
Ctatatan : Data karangan
Hipotesis yang diajukan adalah
H0 : Tidak ada hubungan antara variabel 1 dan variabel 2 atau variabel 1 dan variabel 2 saling bebas (independen)
H1: Tidak ada hubungan antara variabel 1 dan variabel 2 atau variabel 1 dan variabel 2 saling bebas (independen)

Tolak hipotesis nol(H0) jika nilai statistik uji diatas lebih besar dari nilai kritis distribusi chi-square dengan derajat bebas (2-1)(2-1)=1 pada tingkat signifikansi alpha (α) tertentu yang berarti terdapat hubungan antara variabel 1 dengan variabel 2.

Hipotesis nol(H0) ditolak jika nilai statistik uji diatas lebih besar dari nilai kritis distribusi chi-square dengan derajat bebas (I-1)(J-1) pada tingkat signifikansi alpha (α) tertentu yang berarti terdapat hubungan antara variabel 1 dengan variabel 2.
Contoh: Pada liga bola basket professional selama 1980 – 1982, yaitu ketika Larry Bird dari Boston Celtics melakukan lemparan bebas (pada basket lemparan bebas adalah 2 kali lemparan). Catatan lemparan bebas Larry Birds adalah 5 kali dia gagal memasukkan keduanya, 251 kali dia berhasil memasukkan keduanya, 34 kali dia berhasil hanya pada lemparan pertama, dan 48 kali dia berhasil hanya pada lemparan kedua. Apakah masuk akal bahwa lemparan bebas tersebut adalah independen ?
Jawab:
Hal pertama yang harus dilakukan adalah mengidentifikasi bagaimana bentuk tabel yang akan dibuat. Tabel Kontingensi untuk kasus di atas sebagai berikut
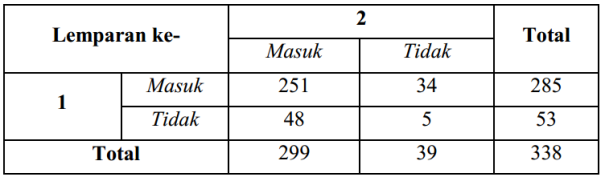
Karena yang ingin dilihat apakah masuk akal mengatakan bahwa lemparan bebas yang dilakukan tersebut saling independen maka pengujian yang dilakukan adalah sebagai berikut:

Uji Statistik (perhitungan) :
Terlebih dahulu hitung frekuensi harapan untuk masing-masing sel pada tabel kontingensi.
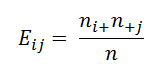
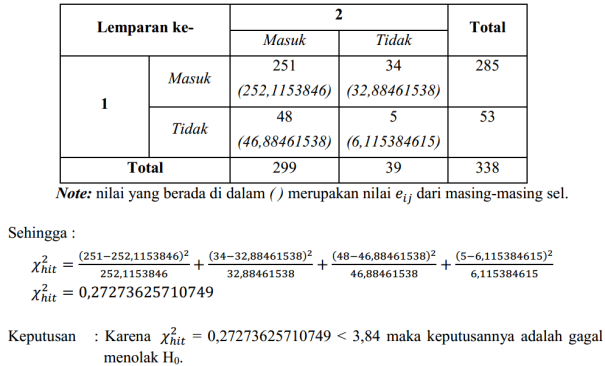
Uji dengan menggunakan Chi-Square seperti yang diatas hanya bisa digunakan jika tidak lebih 20 % frekuensi harapan dari sel yang ada pada tabel kurang dari 5 dan tidak boleh ada satupun dari sel memiliki frekuensi harapan kurang dari 1. Apabila persyaratan diatas tidak bisa terpenuhi, maka kita dapat memperbesar nilai frekuensi harapannya dengan jalan menggabungkan baris atau kolom yang saling berdampingan. Penggabungan yang dilakukan harus secara wajar dan memiliki makna. Namun hal ini tidak dapat diterapkan untuk table kontingensi 2×2, sebagai alternatifnya kita bisa menggunkan Uji Fisher yang memang dikhususkan untuk jumlah sampel yang kecil.
Peniliti biasanya dapat menghindari masalah ini dengan merancang sebelumnya untuk mengumpulkan sejumlah kasus yang cukup besar sehubungan dengan banyak klasifikasi yang ingin digunakan dalam penelitiannya.
Sumber : http://parameterd.wordpress.com/2013/09/13/tabel-kontingensi-cross-classification-table/
Hipotesis yang diajukan adalah
H0 : Tidak ada hubungan antara variabel 1 dan variabel 2 atau variabel 1 dan variabel 2 saling bebas (independen)
H1: Tidak ada hubungan antara variabel 1 dan variabel 2 atau variabel 1 dan variabel 2 saling bebas (independen)

Tolak hipotesis nol(H0) jika nilai statistik uji diatas lebih besar dari nilai kritis distribusi chi-square dengan derajat bebas (2-1)(2-1)=1 pada tingkat signifikansi alpha (α) tertentu yang berarti terdapat hubungan antara variabel 1 dengan variabel 2.

Hipotesis nol(H0) ditolak jika nilai statistik uji diatas lebih besar dari nilai kritis distribusi chi-square dengan derajat bebas (I-1)(J-1) pada tingkat signifikansi alpha (α) tertentu yang berarti terdapat hubungan antara variabel 1 dengan variabel 2.
Contoh: Pada liga bola basket professional selama 1980 – 1982, yaitu ketika Larry Bird dari Boston Celtics melakukan lemparan bebas (pada basket lemparan bebas adalah 2 kali lemparan). Catatan lemparan bebas Larry Birds adalah 5 kali dia gagal memasukkan keduanya, 251 kali dia berhasil memasukkan keduanya, 34 kali dia berhasil hanya pada lemparan pertama, dan 48 kali dia berhasil hanya pada lemparan kedua. Apakah masuk akal bahwa lemparan bebas tersebut adalah independen ?
Jawab:
Hal pertama yang harus dilakukan adalah mengidentifikasi bagaimana bentuk tabel yang akan dibuat. Tabel Kontingensi untuk kasus di atas sebagai berikut

Karena yang ingin dilihat apakah masuk akal mengatakan bahwa lemparan bebas yang dilakukan tersebut saling independen maka pengujian yang dilakukan adalah sebagai berikut:

Uji Statistik (perhitungan) :
Terlebih dahulu hitung frekuensi harapan untuk masing-masing sel pada tabel kontingensi.
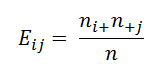

Uji dengan menggunakan Chi-Square seperti yang diatas hanya bisa digunakan jika tidak lebih 20 % frekuensi harapan dari sel yang ada pada tabel kurang dari 5 dan tidak boleh ada satupun dari sel memiliki frekuensi harapan kurang dari 1. Apabila persyaratan diatas tidak bisa terpenuhi, maka kita dapat memperbesar nilai frekuensi harapannya dengan jalan menggabungkan baris atau kolom yang saling berdampingan. Penggabungan yang dilakukan harus secara wajar dan memiliki makna. Namun hal ini tidak dapat diterapkan untuk table kontingensi 2×2, sebagai alternatifnya kita bisa menggunkan Uji Fisher yang memang dikhususkan untuk jumlah sampel yang kecil.
Peniliti biasanya dapat menghindari masalah ini dengan merancang sebelumnya untuk mengumpulkan sejumlah kasus yang cukup besar sehubungan dengan banyak klasifikasi yang ingin digunakan dalam penelitiannya.
Sumber : http://parameterd.wordpress.com/2013/09/13/tabel-kontingensi-cross-classification-table/








Komentar ini telah dihapus oleh pengarang.
BalasHapusMasih gagal paham
BalasHapus